Сочи, Сириус, презентация работы моего кода для построения алгоритмов быстрого матричного умножения.
Приветствую
на моей персональной страничке! Я Александр Осинский, начинающий ученый, на данный момент работаю в Сколтехе. Здесь будет что-то в духе краткого портфолио, где я расскажу немного о тематике моих исследований. Просто хочется создать себе некую идентичность. Я постараюсь дать общий обзор относительно простыми словами. Если Вам будут интересны конкретные результаты, можете посмотреть мой профиль в RESEARCHGATE.
Интересы
МАЛОРАНГОВЫЕ АППРОКСИМАЦИИ МАТРИЦ широко используются для понижения сложности различных вычислений, поскольку какая бы ни стояла физическая или оптимизационная задача, довольно часто в ней присутствует большое количество линейных операций. Крестовая (скелетная) аппроксимация - это особый вид аппроксимации матриц, которая использует небольшое число конкретных строк и столбцов матрицы A, и тем самым основана на небольшом объеме информации. Искусство выбора наилучших строк и столбцов, используя при этом минимум дополнительной информации, лежит в основе крестовых малоранговых алгоритмов аппроксимации.
Мои исследования по большей части направлены на расширение результатов Н. Л. Замарашкина, С. А. Горейнова и Е. Е. Тыртышникова путем улучшения algorithms поиска подматриц максимального объема (и проективного объема) и получения более точных оценок для вычислительной сложности и точности.
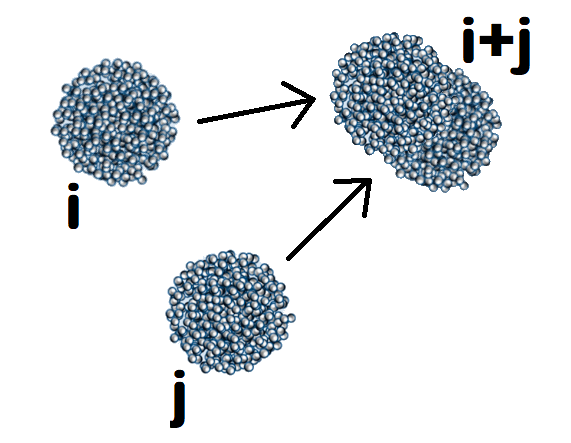
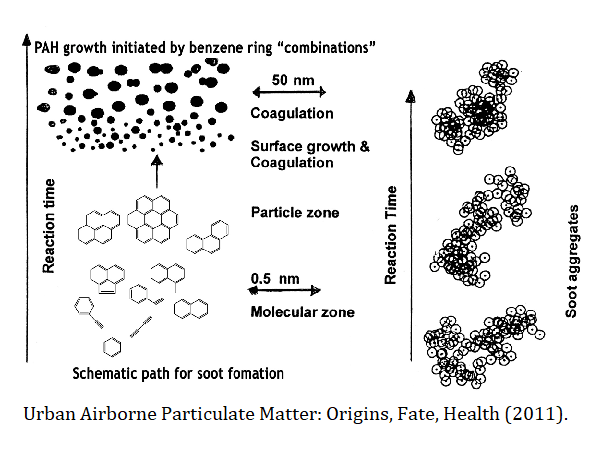
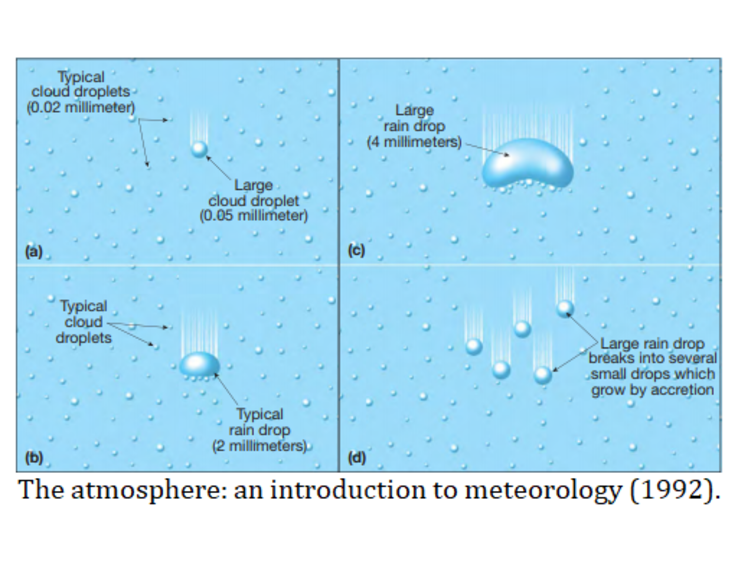
УРАВНЕНИЯ СМОЛУХОВСКОГО описывают процессы агрегации, в которых пары кластеров сталкиваются и образуют кластер большего размера. Они используются для описания широкого круга природных и индустриальных процессов, начиная с самосборки полимеров, формирования дождевых капель и твердых частиц загрязнений и заканчивая эволюцией протопланет и поясов астероидов. Основная сложность при решении уравнений Смолуховского возникает из-за того, что они формируют бесконечную систему дифференциальных уравнений (так как возможно бесконечной число различных размеров кластеров). В результате, их достаточно тяжело решать даже приближенно.
Мои исследования здесь расширяют малоранговый метод решения уравнений Смолуховского, разработанный С. А. Матвеевым, а также направлены на учет изменения кинетических энергий сталкивающихся кластеров в совместных работах с Н. В. Бриллиантовым. В частности, я обобщаю малоранговые методы на температурно-зависимые уравнения Смолуховского и разрабатываю быстрые методы для Монте-Карло моделирования.
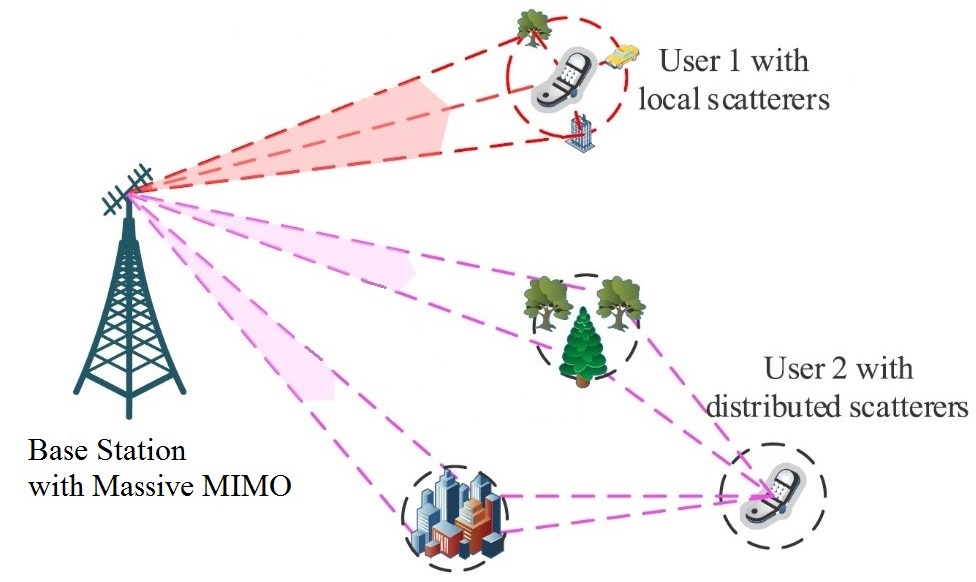
ТЕХНОЛОГИЯ MASSIVE MIMO (multiple input and multiple output, множественный вход и выход) является основным преимуществом 5G по сравнению с предыдущими поколениями сотовой связи. Massive MIMO системы позволяют с высокой точностью находить направление на каждого пользователя от базовой станции, тем самым избегая перекрытия сигнала от разных источников. В то же время, они позволяют использовать информацию от отраженных лучей, что существенно улучшает результат в сценариях без прямой видимости (например, в торговых центрах). Основной трудностью здесь является поиск направлений, соответствующих сигналам текущего пользователя, когда присутствует большой объем шума и интерференции.
Решением задач в данном направлении я занимаюсь вместе с группой А. А. Иванова, я использовал здесь его рисунки. Кроме академических исследований, посвященных в основном проблеме оценки канала, я участвовал (и все еще участвую) в нескольких проектах компании Huawei: о создании эффективных FIR (finite impulse response) фильтров, создании "умного" MIMO приемника, и об ускорении MMSE детектора.
В плане фундаментальных исследований, я изучаю "крестовые малоранговые аппроксимации матриц". Давайте подробно рассмотрим, что же это такое.
Для начала, я без зазрения совести назову любой 2D-массив (таблицу) чисел матрицей. Очевидно, что следует также добавить, как минимум, как именно разрешено работать с матрицами, т.е. определить еще и операции. Нас в первую очередь будет интересовать матричное умножение (вики). Будем считать, что Вы знаете, что это такое (иначе, пожалуйста, посмотрите). Итак, почему же оно так важно? Как видно из определение, если, скажем, нам дана $M \times N\;$матрица, мы можем попытаться записать ее в виде произведения$\;M \times r\;$и$\;r \times N\;$матриц (см. ниже).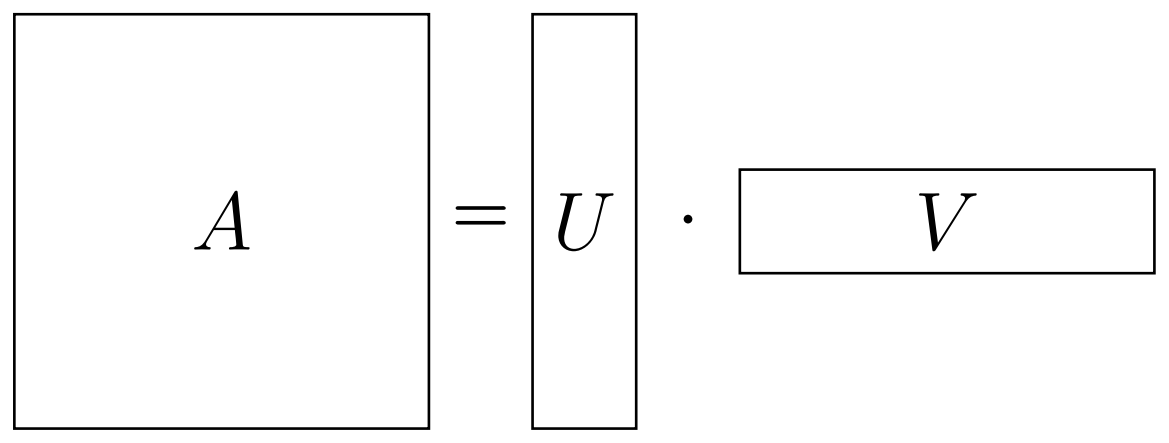
Если удалось найти такое "разложение" с небольшим$\;r$, тогда его можно назвать "малоранговым" (наименьшее$\;r\;$называется "рангом") разложением нашей матрицы$\;A$. А в случае, если равенство не является точным, назовем это "малоранговой аппроксимацией". Должно быть, Вы уже видите, чем такое разложение может быть полезно: у нас может быть огромная матрица$\;A$, но при этом "факторы"$\;U\;$и$\;V\;$довольно тонкие. В результате, мы не только экономим память, но и сокращаем стоимость любых операций над факторами разложения.
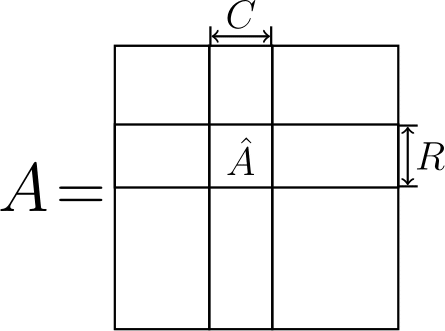
Теперь встает вопрос, как нам получить факторы$\;U\;$и$\;V$? Здесь и вступает в игру "крестовый" метод. А именно, есть довольно простой способ выбора данных факторов: достаточно использовать$\;U = C\;$и$\;V = \hat A^{-1} R$, где$\;C\;$– некоторые$\;r\;$столбцов матрицы$\;A$,$\;R\;$– некоторые$\;r\;$ее строк, а$\;\hat A^{-1}\;$– обратная к матрице на пересечении$\;C\;$и$\;R\;$(помните тот рисунок выше? Давайте я снова его покажу, чтобы было понятней).
Если разложение является точным, то нет особого значения, какие строки и столбцы выбирать. Однако, если это не так, то погрешность аппроксимации сильно зависит от выбранных строк и столбцов. Хорошей идеей оказывается поиск подматрицы $\hat A\;$(и, автоматически, ее строк$\;R\;$и столбцов$\;C$) с большим "объемом" (модулем "определителя" матрицы). Все это было известно еще до того, как я начал обучаться в бакалавриате.
Чем же я тогда занимаюсь? До этого я рассматривал случай, когда число строк и столбцов совпадает с рангом аппроксимации $r$. Но что если мы выберем больше? Существует ли относильно простой способ улучшить точность аппроксимации, не увеличивая при этом ее итоговый ранг?
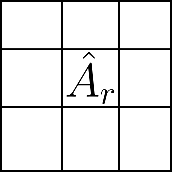
И такой способ есть. Чтобы добиться улучшения, вместо поиска подматрицы большого "объема", следует искать подматрицу большого "проективного объема" (равного произведению первых$\;r\;$ее сингулярных чисел) и сделать псевдообращение, оставив только их, используя сингулярное разложение (вики). Это "оставляем первые$\;r\;$сингулярных чисел" обозначается индексом$\;r\;$и будет моей невидимой (потому что она очень маленькая) иконкой сайта.
Поскольку мы таким образом изменяем лишь небольшую подматрицу $\hat A$, это совсем не затратно с точки зрения вычислительных ресурсов, но при этом позволяет приблизиться сколь угодно близко к оптимальной аппроксимации по Фробениусовой (евклидовой) норме. В своих статьях я показываю, что данный подход (часто) работает, а также предлагаю способы быстро найти подматрицу с большим проективным объемом.
Здесь мне понадобиться быть немного техничным, прошу не уходить сразу.
Агрегация в гранулярных газах (да и любой другой системе) описывается системой уравнений Смолуховского
$$ \frac{dn_k}{dt} = \frac{1}{2} \mathop{ \sum}\limits_{i+j=k} C_{ij} n_i n_j - \mathop{ \sum}\limits_j C_{kj} n_k n_j.$$
Каждое уравнение является дифференциальным и описывает скорость изменения концентраций (плотностей числа частиц)$\;n_k\;$для частиц размера$\;k$. В простейшем случае$\;k\;$является целым числом, которое задает размер кластера. В правой части равенства считается полное число столкновений на основе их частот$\;C_{ij}$. А именно, число столкновений между кластерами размера$\;i\;$и$\;j\;$пропорционально числу кластеров размера$\;i$,$\;n_i$, числу кластеров размера$\;j$,$\;n_j$ и тому, как часто каждая пара сталкивается: эта частота и обозначается как$\;C_{ij}$. Мы умножаем на$\;\frac{1}{2}\;$, чтобы компенсировать двойной учет пар$\;(i,j)\;$вместе с$\;(j,i)\;$ (ведь это одна и та же пара). Таким образом, первая сумма дает нам число появившихся кластеров размера$\;k = i + j$. Однако, кластеры размера$\;k\;$сами агрегируют и формируют еще большие кластеры, так что нужно затем вычесть их число, участвующее в столкновениях с кластерами произвольного размера$\;j$, что дает нам вторую сумму.
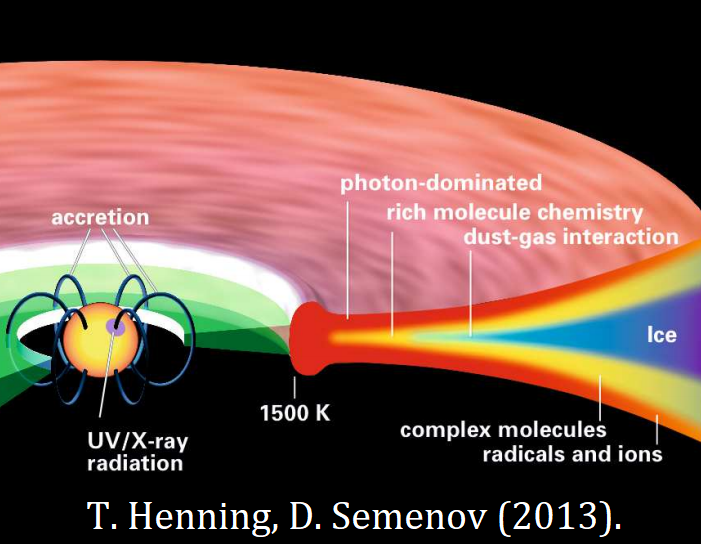
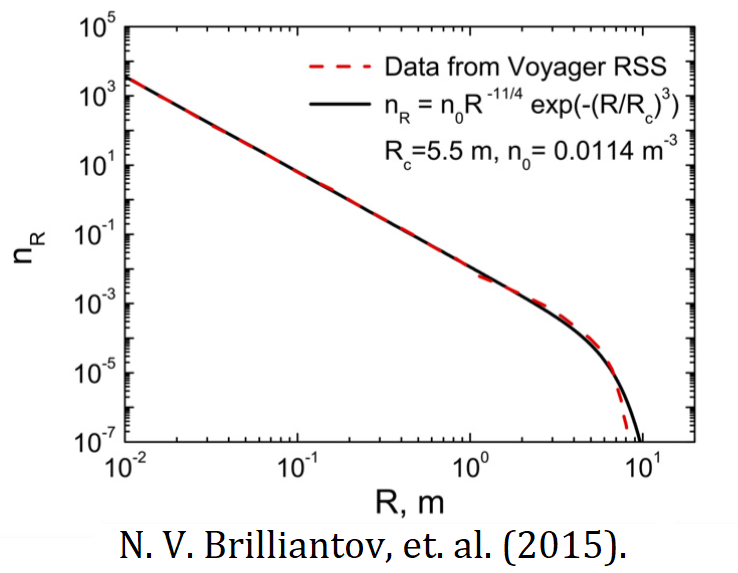
Как упоминалось ранее, это бесконечная система (так как существует бесконечное число целых чисел$\;k$). На практике, когда мы ограничиваем себя конченым числом уравнений, это число все равно может достигать миллионов, если мы хотим относительно точно описать весь гранулярный газ. Например, для частиц пыли в протопланетных дисках (см. модельный пример на рисунке ниже), диаметр может составлять от микрометра до сантиметра, а их массы охватывают около десяти порядков.
К счастью, существуют быстрые малоранговые методы для решения уравнений Смолуховского, разработанные Сергеем Матвеевым и соавторами. Я тоже участвовал в совершенствовании этих методов, чтобы они успешно работали для частот$\;C_{ij}$, меняющихся со временем.
Однако, существует способ в принципе обойти прямое решение этих сложных уравнений. Чтобы это сделать, достаточно провести Монте-Карло моделирование: создается конечная система виртуальных частиц, оценивается частота их столкновений, и данные столкновения выполняются. С уменьшением числа частиц в результате агрегации, можно просто удвоить их число, оставив то же соотношение между частицами различного размера. Эта идея используется для моделирования произвольных смесей газов (в том числе и без агрегации) и позволяет также исследовать скорости частиц каждого размера. Чтож, раз мы можем просто моделировать столкновения, а не решать уравнения, в чем же проблема?
А проблема состоит в том, как нам определить, кто когда сталкивается. Конечно, все эти частоты нам известны – мы их обозначили как$\;C_{ij}$. Но, чтобы определить следующее столкновение, нам нужно знать все$\;N^2\;$частот, если у нас$\;N\;$различных размеров. Точнее, нам нужно знать$\;N^2\;$значений$\;C_{ij} n_i n_j$, а они меняются после каждого столкновения, поскольку меняется количество (а потому и концентрация) частиц каждого размера. А если мы используем более сложный вариант моделирования, где напрямую учитываются скорости частиц, то частоты будут меняться и с изменением скоростей. Обновлять их после каждого столкновения чересчур затратно: если меняется концентрация одного размера, то обновляются все$\;N\;$ частот, где этот размер присутствует.
К счастью, существует способ сделать обновление (и выбор пары сталкивающихся частиц) существенно быстрее (за логарифмическое по числу размеров время). И этот способ, стоит подчеркнуть, работает также и для систем без агрегации. Хотя он также основан на малоранговом разложении, сама матрица$\;C_{ij}\;$ не обязана быть малоранговой: достаточно иметь возможность сделать для нее малоранговую оценку сверху (что возможно для всех известных мне примеров, даже таких экзотических, как агрегация прямоугольников).
К сожалению, я не могу описать ее здесь более детально, поскольку все еще работаю над статьей. Но, напомню, чуть более подробное описание моих идей доступно здесь.
Так как я в основном занимался оценкой канала, то поговорим тут о ней.
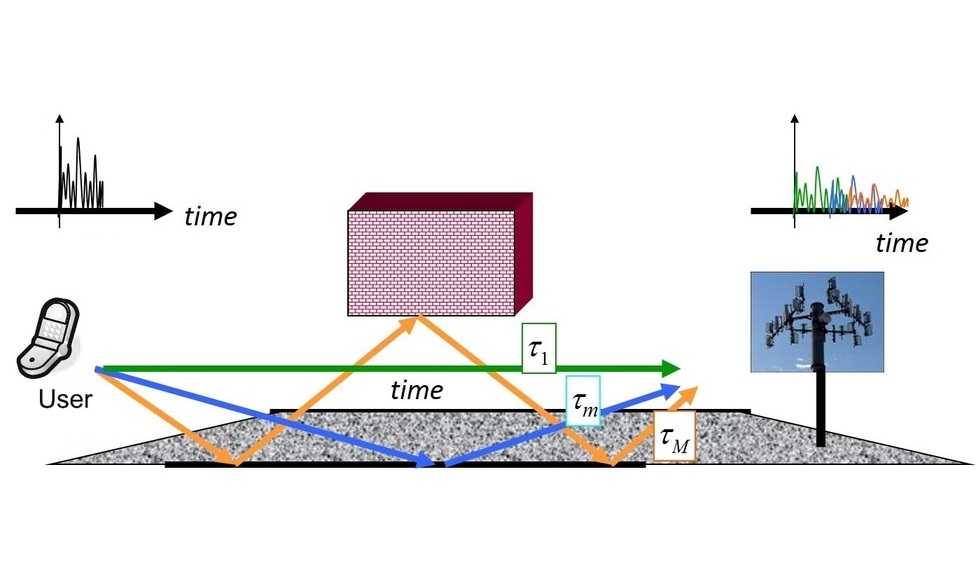
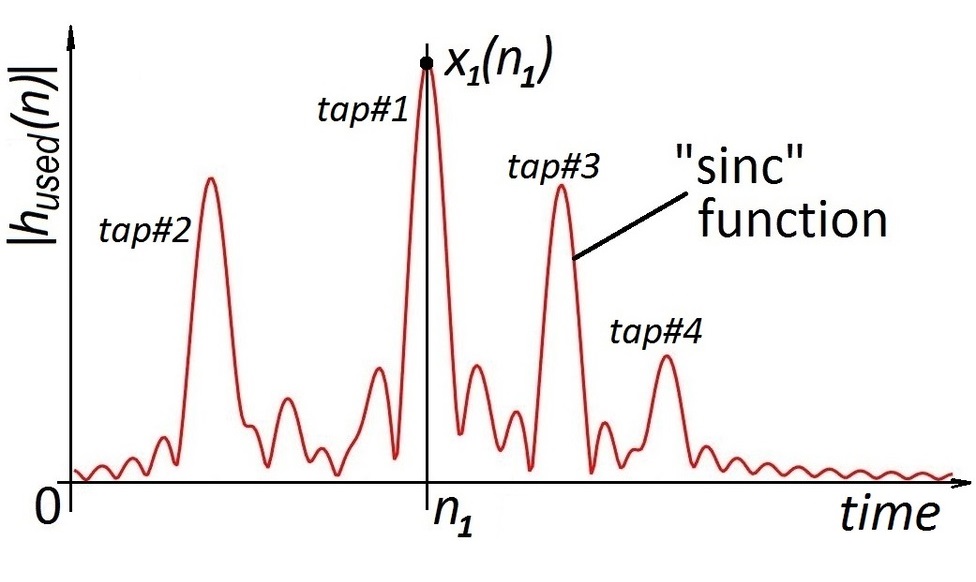
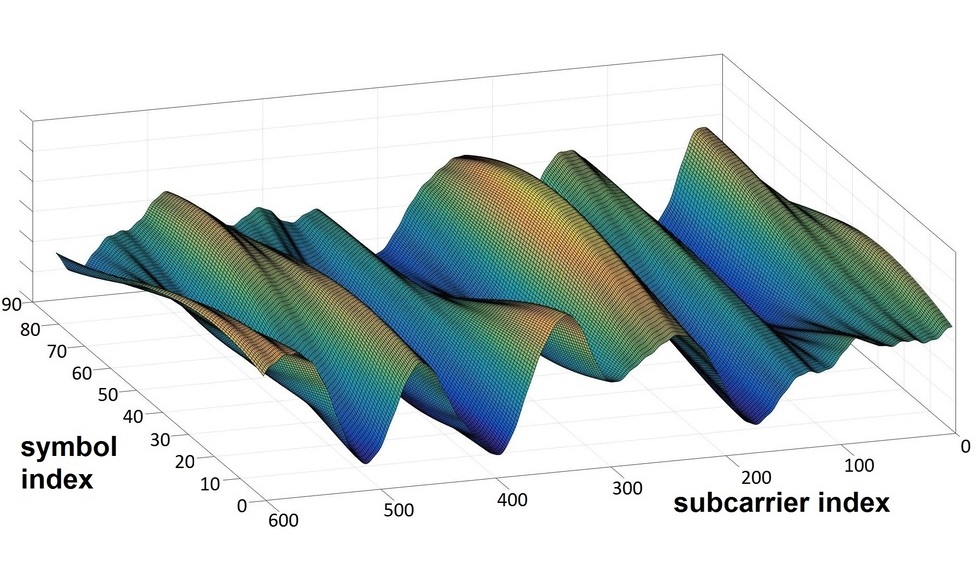
При оценке канала связи пользователь отсылает на базовую станцию заранее известный сигнал (называемый пилотным или просто пилотом), чтобы определить, как именно он изменяется при передаче. В идеале, нам нужно поймать также все источники отраженных сигналов, которые соответствуют максимумам на рисунке ниже. Пики (соответствующие различным моментам времени, в которые был получен сигнал) на нем сглажены из-за использования oversampling'а: на практике сигнал измеряется не непрерывно, а в определенные моменты времени. Oversampling позволяет более точно определить момент получения сигнала, но при этом превращает дискретный пики в "sinc" функции. Примеры полученного сигнала (в отсутствиии шума) показаны ниже:
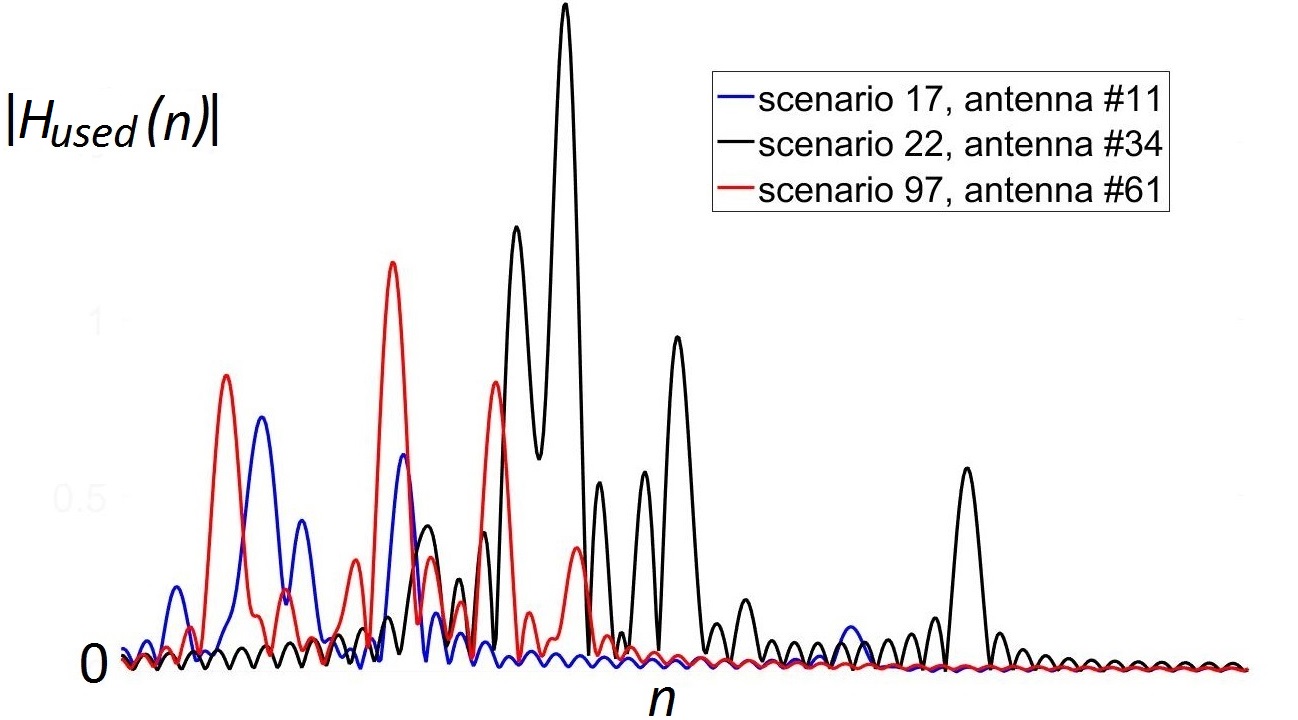
Основной идеей нашего метода было найти максимумы и подставить в эти точки "sinc" функции. Если сделать это поочередно для всех максимумов, то сигнал будет полностью восстановлен.
В реальности, однако, мы не можем оставить вообще все точки максимума, поскольку уровень шума примерно такой же, как и уровень мощности сигнала. В результате, некоторые "пики" на самом деле лишь случайные выбросы шума, и нужно определить, какие из найденных максимумов стоит оставлять в оценке.
В основе наших алгоритмов лежит довольно простая идея, что, на мой взгляд, делает ее довольно интересной. Во-первых, мы оставляем только те пики, чья полная мощность$\;\| y \|^2\;$превосходит мощность шума$\;\sigma^2$. Как оказалось, это почти оптимальный выбор, если сделать кое-что еще.
А именно, после выбора каждого пика, его значение взвешивается на величину$\;1 - \frac{\sigma^2}{\| y \|^2}$. Если вам знакомо оценивание с минимальной средеквадратичной ошибкой (MMSE), которое приводит к взвешиванию вида$\;\frac{1}{1 + \frac{\sigma^2}{\| x \|^2}}\;$, то должно быть легко увидеть сходства. На самом деле, это, в некотором смысле, та же самая оценка:$\;\| x \|^2\;$— это ожидаемая мощность сигнала без шума, так что (в среднем) полная мощность принятого сигнала как раз равна$\;\| y \|^2 = \| x \|^2 + \sigma^2$, что при подстановке и приводит к используемому нами взвешиванию.
"Но постойте!" – могут сказать те, кто слишком хорошо знают теорию вероятности, – "MMSE применим только если заранее известна дисперсия сигнала (в данном случае равняющаяся его ожидаемой мощности$\;\|x\|^2$). А она-то не известна! И ее нельзя брать из того же самого единственного значения, которые нам и нужно оценить! В таком случае необходимо использовать несмещенную оценку." И вы будете правы. Формально. За исключением того, что мощность все-таки можно оценить из этого единственного значения, посколько оно известно сразу на многих антеннах, которые, хоть и коррелированы, имеют одинаковое распределение. Указанное выше взвешивание является в определенном смысле оптимальным и работало вообще во всех сценариях, которые нам встречались.
Это довольно простой результат, который может быть использован всегда, когда известно распределение шума, но не самих данных, но при этом я его почему-то нигде не встречал. Для меня он интересен тем, что как будто бы не использует никакой априорной информации о данных, но при этом следует из байесовской оценки, для которой такая информация необходима.
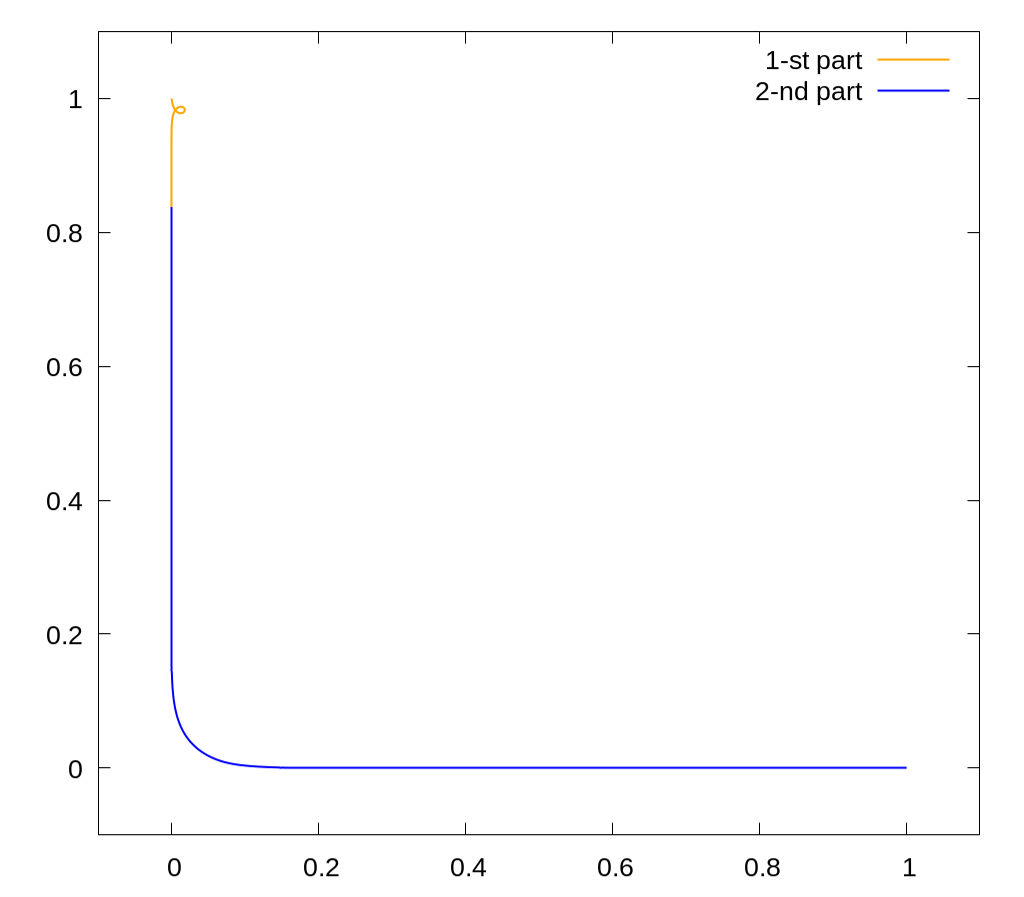
Это кратчайшая кривая, начинающаяся в точке $(1,0)$, заканчивающаяся в $(0,1)$, и такая, что $\int xy \, dx \, dy = 0$ под ней. Длина кривой примерно равна $1.9881$.
Сложность здесь заключалась в том, что это задача не решается методом стрельбы, даже с использованием принципа максимума Понтрягина.
Тем не менее, мной был найден способ решения данной задачи и даже был опубликован код, строящий данную кривую.
Награды
Золотая медаль Российской Академии Наук
Кроме того, что моя магистерская диссертация была удостоена золотой медали, мне также удалось пару раз получить диплом победителя на конференции МФТИ, пока я там учился.
